terça-feira, 6 de abril de 2010

Médias Aritméticas e Números Significativos

Há dois tipos de média aritmética - simples ou ponderada.

  • Média aritmética simples

A média aritmética simples é a mais utilizada no nosso dia-a-dia. É obtida dividindo-se a soma das observações pelo número delas. É um quociente geralmente representado pelo símbolo 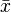\bar{x}. Se tivermos uma série de n valores de uma variável x, a média aritmética simples será determinada pela expressão:

\bar{x} = \frac{x_1 + x_2 + .. .. + x_n}{n} = {1 \over n} \sum_{i = 1}^n{x_i}


  • Média aritmética ponderada

Consideremos uma coleção formada por n números: 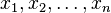x_1, x_2, \ldots, x_n, de forma que cada um esteja sujeito a um peso [Nota: "peso" é sinónimo de "ponderação"], respectivamente, indicado por: 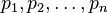p_1, p_2, \ldots, p_n. A média aritmética ponderada desses n números é a soma dos produtos de cada um multiplicados por seus respectivos pesos, dividida pela soma dos pesos, isto é:

\bar{x} = \frac{x_1 p_1 + x_2 p_2 + .. .. + x_n p_n}{p_1 + p_2 + .. .. + p_n}

Obviamente, a média aritmética e a média ponderada podem ser generalizadas para estruturas algébricas mais complexas; a única restrição é que a soma dos pesos seja um número invertível (em particular, não pode ser zero).

Exemplos

  • Um aluno tirou as notas 5, 7, 9 e 10 em quatro provas. A sua média será (5 + 7 + 9 + 10) / 4 = 7.75
  • Um aluno fez um teste (peso 1) e uma prova (peso 2), tirando 10 no teste e 4 na prova. A sua média (ponderada) será (10 x 1 + 4 x 2) / (1 + 2). Teríamos então: (10 + 8) / 3. Logo, o resultado da média aritmética ponderada para este exemplo é: 6. Se o teste e a prova tivessem mesmo peso (e não importa qual o valor do peso, importa apenas a relação entre os pesos), a média ponderada aritmética seria sempre 7. Isto é, se o aluno fizesse um teste (peso 3) e uma prova (peso 3) obtendo respectivamente a mesma pontuação anterior (10 e 4), teríamos: (10 x 3 + 4 x 3) / (3 + 3). Continuando: (30 + 12) / 6. O resultado para pesos iguais será sempre: "7". Veja: (30 + 12) / 6 = 7.
  • Um triângulo no plano tem vértices dados pelas coordenadas cartesianas (2, 1), (4, -1) e (3, 6). O seu baricentro é a média dos vértices, ou seja (3, 2).
Números significativos

Na IT matemática aplicada, algarismos significativos são utilizados para monitorar os erros ao se representar números reais na base 10.

Diz-se que uma representação tem n algarismos significativos quando se admite um erro no algarismo seguinte da representação. Por exemplo, 1/7 = 0,14 com dois algarismos significativos (já que o erro está na terceira casa decimal: 1/7 = 0,142857142857...). Analogamente, 1/30 = 0,0333 com três algarismos significativo (erro na quinta casa decimal).

Para ilustrar, imagine que você pediu a um amigo para medir a temperatura de água e disse a você que esta se encontrava à 22,0° C. Neste caso, o algarismo duvidoso é o 0, pois não se sabe ao certo se a temperatura é por exemplo, 21,99 ou 22,01. Em suma isto se remete ao fato dos arredondamentos serem realizados e nem sempre serem conhecidos. Para entender este conceito, imagine que seu amigo lhe contou que na realidade a medição foi de 25,689. Nesse contexto pode-se introduzir o conceito de precisão e exatidão. 22 é um número exato, porém 25,689 é um número mais preciso, você precisará do valor preciso para realizar um cálculo matemático, por exemplo, mas didaticamente se adota o 22.

Identificando algarismos significativos

Dada uma representação decimal:

  1. os algarismos zero que correspondem às ordens maiores não são significativos. Exemplos: em 001234,56 os dois primeiros zeros não são significativos; em 0,000543 os quatro primeiros zeros não são significativos
  2. os algarismos zero que correspondem às menores ordens, se elas são fracionárias, são significativos. Exemplo: em 12,00 os dois últimos zeros são significativos
  3. os algarismos de 1 a 9 são sempre significativos
  4. zeros entre algarismos de 1 a 9 são significativos. Exemplo: em 1203,4 todos algarismos são significativos
  5. os zeros que completam números múltiplos de potências de 10 são ambíguos: a notação não permite dizer se eles são ou não significativos. Exemplo: em 120300, os quatro primeiros algarismos (1,2,0,3) são significativos, e não é possível dizer se os dois últimos zeros são significativos. Esta ambiguidade deve ser corrigida, usando-se Notação científica para representar estes números.

Outros exemplos:

  • 0,5: tem 1 algarismo significativo;
  • 100: é Não Determinado (ND), pois acaba com um zero à direita do último dígito que não seja zero, sem a pontuação décimal; (necessita de referência)
  • 0,00023: tem dois algarismos significativos, que são 23;
  • 052,6: tem 3 algarismos significativos;
  • 0,000200: tem três algarismos significativos, já que zeros à direita são significativos, 200;
  • 755555,66: tem 8 algarismos significativos, porque 7,5 é um valor maior que 5.

A posição da vírgula não influi no número de algarismos significativos, por exemplo, o comprimento de 0,0240m possui três algarismos significativos e pode ter a posição da vírgula alterado de várias formas usando uma potência de dez adequada, e sem alterar o seu número de algarismos significativos. Veja abaixo:

0,0240\,m = 0,240 \times 10^{-1}\,m = 0,240\,dm

0,0240\,m = 2,40 \times 10^{-2}\,m = 2,40\,cm

0,0240\,m = 24,0 \times 10^{-3}\,m = 24,0\,mm

Observe que o número de algarismos significativos é sempre três, independentemente da forma que o número foi escrito e da posição de sua vírgula. Outro ponto importante é que o valor da medida é sempre a mesma, visto que: 0,0240m = 0,240dm = 2,40 cm = 24,0mm.

Operações com algarismos significativos

Soma e subtração

Quando somamos dois números levando em consideração os algarismos significativos o resultado deve manter a precisão do operando de menor precisão.

12,56 + 0,1236 = 12,6836 = 12,68

O número 12,56 tem quatro algarismos significativos e o último algarismo significativo é o seis que ocupa a casa dos centésimos. O número 0,1236 apresenta quatro algarismos significativos mas o último algarismo significativo, o seis ocupa a casa dos décimos de milésimos. O último algarismo significativo do resultado deve estar na mesma casa do operando de menor precisão, nesse exemplo é o 12,56. Portanto o último algarismo significativo do resultado deve estar na casa dos centésimos.

Multiplicação e divisão

Em uma multiplicação levando em consideração os algarismos significativos o resultado deve ter o mesmo número de algarismos significativos do operando com a menor quantidade de algarismos significativos.

3,1415x180 = 5,65x102

O número 180 apresenta três algarismos significativos, 1, 8 e 0, lembrando que o zero à direita deve ser contado como significativo, enquanto que o à esquerda não o deve. Mas o número 3,1415 apresenta cinco algarismos significativos os 31415. O resultado deve ter apenas três algarismos significativos, os 565.

Logarítmos

Ao se trabalhar com logarítmos, observa-se o número de algarismos significativos do argumento e o total de casas depois da vírgula do logarítmo é igual a esse número.

ln(5,0 * 103) = 8,52 2 significativos no argumento→ 2 casas decimais no logarítmo.

ln(45,0) = 3,807 3 significativos no argumento→ 3 casas decimais no logarítmo.

Postado por às

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)